R
Εισαγωγη στην R
Απλή Γραμμική Παλινδρόμηση με την R
Άννα Μοσχά Κέντρο Η/Υ, Ε.Μ.Π.
Περιεχομενα
- Συσχέτιση δύο ποσοτικών μεταβλητών
- Απλή Γραμμική Παλινδρόμηση με την R
- Προϋποθέσεις απλού γραμμικού μοντέλου
- Παράδειγμα Απλής Γραμμικής Παλινδρόμησης με την R
Συσχέτιση δύο ποσοτικών μεταβλητών
- Πολλές φορές δύο ποσοτικές μεταβλητές σχετίζονται μεταξύ τους, όπως το βάρος και η ηλικία ενός παιδιού, η ταχύτητα ενός αυτοκινήτου και η απόσταση που απαιτείται για να ακινητοποιηθεί.
- Η πιο απλή μορφή συσχέτισης είναι η γραμμική με την οποία θα ασχοληθούμε.
- Ο πιο απλός τρόπος να δούμε αν δύο ποσοτικές μεταβλητές σχετίζονται μεταξύ τους είναι να κάνουμε το διάγραμμα της διασποράς τους.Το διάγραμμα είναι απαραίτητο να γίνει για να δούμε αν υπάρχει σχέση μεταξύ τους και σε περίπτωση που υπάρχει αν είναι γραμμική.
Συσχέτιση δύο ποσοτικών μεταβλητών
- Παράδειγμα: Ας θυμηθούμε το dataframe cars που περιλαμβάνει δύο ποσοτικές μεταβλητές, την ταχύτητα του αυτοκινήτου και την απόσταση που απαιτείται για να ακινητοποιηθεί:
> data(cars)
> str(cars)
'data.frame': 50 obs. of 2 variables:
$ speed: num 4 4 7 7 8 9 10 10 10 11 ...
$ dist : num 2 10 4 22 16 10 18 26 34 17 ...Συσχέτιση δύο ποσοτικών μεταβλητών
- Το διάγραμμα διασποράς των μεταβλητών speed και dist:
> plot(cars$speed, cars$dist, main="Speed versus Stopping distance", pch=16, col=2, xlab="Speed", ylab="Stopping Distance")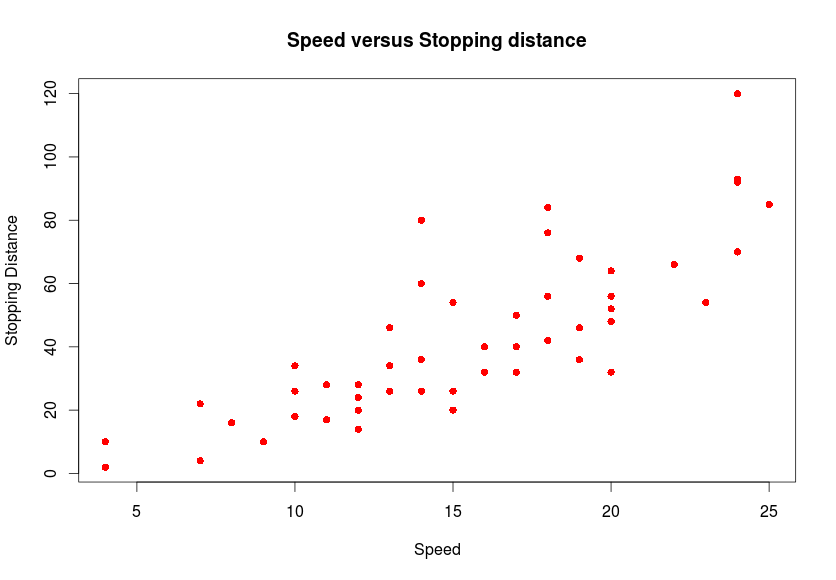
Παρατηρούμε ότι φαίνεται να υπάρχει μία γραμμική συσχέτιση μεταξύ της ταχύτητας και της απόστασης που απαιτείται ως την ακινητοποίηση του αυτοκινήτου.
Συσχέτιση δύο ποσοτικών μεταβλητών
- Ένα μέτρο που μας επιτρέπει να δούμε αν δύο ποσοτικές μεταβλητές Χ και Υ μεταβάλλονται μαζί είναι η συνδιακύμανση (covariance) των δύο μεταβλητών. Ο αντίστοιχος δειγματικός δείκτης δίνεται από τον τύπο: \[ S_{XY}=\frac{1}{n-1}\displaystyle\sum_{i=1}^{n} ({X_i-\overline{X}})({Y_i-\overline{Y}}) \]
- Μηδενικές τιμές της συνδιακύμανσης υποδεικνύουν ότι δεν υπάρχει γραμμική συσχέτιση μεταξύ των μεταβλητών, ενώ το πρόσημο του δείκτη υποδεικνύει θετική (αύξουσα) ή αρνητική (φθίνουσα) σχέση μεταξύ των δύο μεταβλητών.
Συσχέτιση δύο ποσοτικών μεταβλητών
- Η συνδιακύμανση (covariance) δύο μεταβλητών στην R υπολογίζεται με τις εντολές var και cov. Για το παράδειγμα μας έχουμε:
> var(cars$speed,cars$dist)
[1] 109.9469
> cov(cars$speed,cars$dist)
[1] 109.9469Συσχέτιση δύο ποσοτικών μεταβλητών
- Ο δείκτης που μας δίνει το βαθμό γραμμικής συσχέτισης είναι ο συντελεστής γραμμικής συσχέτισης του Pearson, correlation coefficient που δίνεται από το τύπο \[ ρ=\frac{Cov(XY)}{\sqrt{{Var(X)}{Var(Y)}}}, -1 ≤ ρ ≤ 1 \] ενώ ο αντιστοιχος δειγματικός συντελεστής, από τον τύπο: \[ r=\frac{\displaystyle\sum_{i=1}^{n} ({X_i-\overline{X}})({Y_i-\overline{Y}})}{\sqrt{{\displaystyle\sum_{i=1}^{n} ({X_i-\overline{X}})^2}{\displaystyle\sum_{i=1}^{n} ({Y_i-\overline{Y}})^2}}}, -1 ≤ r ≤ 1 \]
Συσχέτιση δύο ποσοτικών μεταβλητών
- Μηδενικές τιμές του συντελεστή συχέτισης υποδεικνύουν ότι οι δύο μεταβλητές είναι μη συσχετισμένες γραμμικά (όχι ανεξάρτητες), τιμές κοντά στην μονάδα (ή στο -1) δείχνουν τέλεια θετική συσχέτιση (αντίστοιχα αρνητική συχέτιση).
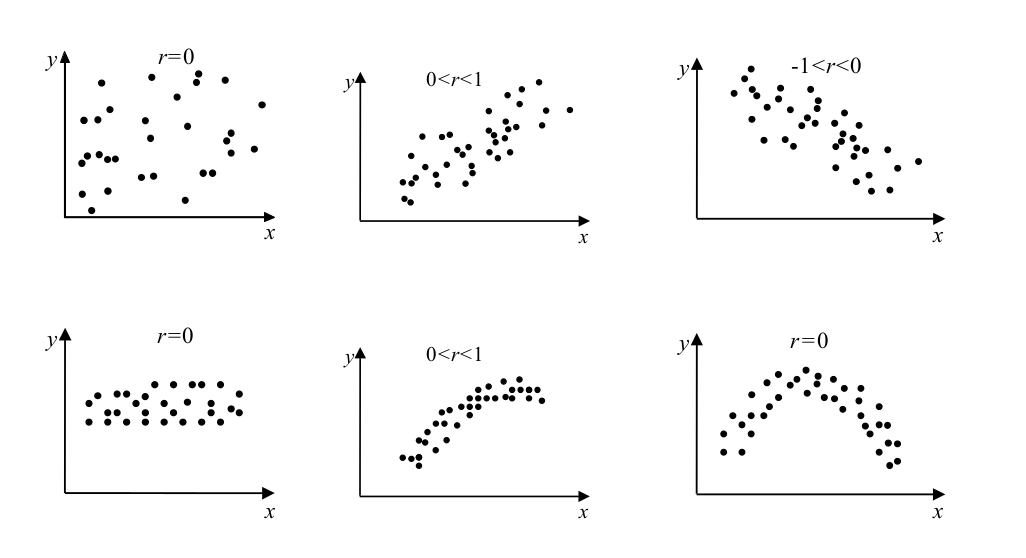Οι παραπάνω εικόνες μας δείχνουν την συσχέτιση σε σχέση με την τιμή του r.
Συσχέτιση δύο ποσοτικών μεταβλητών
- Μη παραμετρικοί δείκτες συχέτισης:
- Ο δείκτης συσχέτισης του Spearman χρησιμοποιεί τα ranks των δεδομένων και δείχνει την ύπαρξη μονότονης (δηλ. όχι απαραίτητα γραμμικής) συσχέτισης.
- Ο δείκτης συσχέτισης του Kendall χρησιμοποιεί λιγότερη πληροφορία και δείχνει την ύπαρξη μονότονης (δηλ. όχι απαραίτητα γραμμικής) συσχέτισης.
- Όλοι οι δείκτες έχουν νόημα να υπολογιστούν ακόμα κι αν δεν ισχύει η κανονικότητα.
- Μηδενικές τιμές των δεικτών δεν σημαίνει απαραίτητα και την υπάρξη ανεξαρτησίας, αλλά μη γραμμική ή μη μονότονη σχέση.
Συσχέτιση δύο ποσοτικών μεταβλητών
- Για το παράδειγμα μας έχουμε:
> cor(cars$speed, cars$dist)
[1] 0.8068949
> cor(cars$speed, cars$dist, method = "spearman")
[1] 0.8303568
> cor(cars$speed, cars$dist, method = "kendall")
[1] 0.6689901Συσχέτιση δύο ποσοτικών μεταβλητών
- Μπορεί να γίνει στατιστικός έλεγχος κατά πόσο δύο τ.μ. Χ και Υ είναι ασυσχέτιστες ή όχι, δηλαδή μπορώ να ελέγξω \(Η_0: ρ=0\) έναντι της \(Η_1: ρ \neq 0\).
- Το στατιστικό που χρησιμοποιώ είναι το \[ Τ=\frac{r}{\sqrt{1-r^2}}\sqrt{n-2}\sim St(n-2)\]
- Στην R ο έλεγχος αυτός γίνεται με την εντολή:
όπου ανάλογα με την μέθοδο που χρησιμοποιώ κάνω παραμετρικό (pearson) ή μη παραμετρικό έλεγχο (spearman, kendall).cor.test(x, y, alternative = c("two.sided", "less", "greater"), method = c("pearson", "kendall", "spearman"), exact = NULL, conf.level = 0.95, continuity = FALSE, ...)
Συσχέτιση δύο ποσοτικών μεταβλητών
- Γραφικός έλεγχος κανονικότητας των μεταβλητών του παραδείγματος για την ταχύτητα του αυτοκινήτου και την απόσταση ακινητοποίησης του:
> par(mfrow=c(2,2))
> hist(cars$speed)
> qqnorm(cars$speed)
> qqline(cars$speed)
> hist(cars$dist)
> qqnorm(cars$dist)
> qqline(cars$dist)
> par(mfrow=c(1,1))Συσχέτιση δύο ποσοτικών μεταβλητών
- Γραφικός έλεγχος κανονικότητας των μεταβλητών του παραδείγματος:
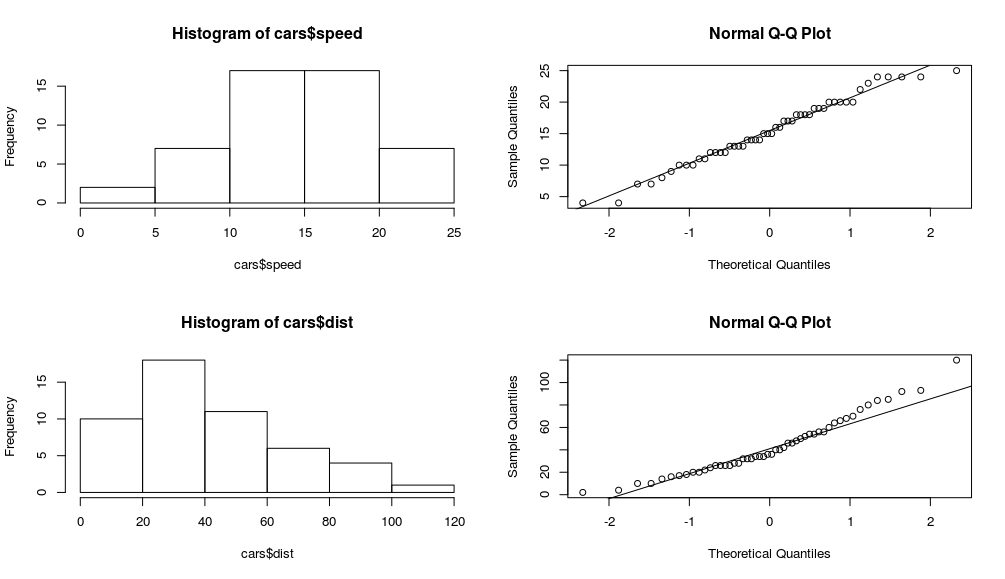Παρατηρούμε ότι η μεταβλητή speed φαίνεται να ακολουθεί κανονική κατανομή αλλά η μεταβλητή dist μπορεί να μην ακολουθεί κανονική κατανομή.
Συσχέτιση δύο ποσοτικών μεταβλητών
- Έλεγχος κανονικότητας των μεταβλητών του παραδείγματος:
> library("nortest")
> lillie.test(cars$speed)
Lilliefors (Kolmogorov-Smirnov) normality test
data: cars$speed
D = 0.068539, p-value = 0.8068
> lillie.test(cars$dist)
Lilliefors (Kolmogorov-Smirnov) normality test
data: cars$dist
D = 0.12675, p-value = 0.04335Συσχέτιση δύο ποσοτικών μεταβλητών
- Για το παράδειγμα μας έχουμε:
> cor.test(cars$speed, cars$dist)
Pearson's product-moment correlation
data: cars$speed and cars$dist
t = 9.464, df = 48, p-value = 1.49e-12
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.6816422 0.8862036
sample estimates:
cor
0.8068949
> cor.test(cars$speed,cars$dist, method="spearman")
Spearman's rank correlation rho
data: cars$speed and cars$dist
S = 3532.8, p-value = 8.825e-14
alternative hypothesis: true rho is not equal to 0
sample estimates:
rho
0.8303568
Warning message:
In cor.test.default(cars$speed, cars$dist, method = "spearman") :
Cannot compute exact p-value with tiesΑπλή Γραμμική Παλινδρόμηση με την R
- Στις περιπτώσεις συσχέτισης δύο ποσοτικών μεταβλητών Χ και Υ, ενδιαφερόμαστε να προβλέψουμε την τιμή της μιας μεταβλητής Υ (μεταβλητή απόκρισης ή ανεξάρτητη μεταβλητή) όταν είναι γνωστή η τιμή της άλλης μεταβλητής Χ (επεξηγηματική μεταβλητή ή εξαρτημένη μεταβλητή).
- Στόχος είναι η κατασκευή ενός κατάλληλου μοντέλου που να μας επιτρέπει την παραπάνω πρόβλεψη.
- Στην περίπτωση που οι δύο μεταβλητές σχετίζονται γραμμικά τότε η σχέση τους δίνεται από την ευθεία γραμμικής παλινδρόμισης που είναι ο απλούστερος τύπος μοντέλου: \[Υ = a + bΧ \]
Απλή Γραμμική Παλινδρόμηση με την R
- Αν η ανάλυση μας γίνεται με βάση ένα δείγμα το μοντέλο μας είναι στοχαστικό ενώ αν βασιζόταν σε ολόκληρο πληθυσμό το μοντέλο θα ήταν προσδιοριστικό.
- Στα στοχαστικά μοντέλα υπάρχει πάντα ένα σφάλγμα ε γιατί έχουμε ελλιπή πληροφορία και το απλό γραμμικό μοντέλο έχει τη μορφή: \[Υ = a + bΧ + ε , \] όπου \( ε\) είναι το τυχαίο σφάλμα με \( ε \sim Ν(0, σ^2) \). Ή ισοδύναμα: \[Ε(Υ|X=x) = a + bΧ \] (το σφάλμα έχει ενσωματωθεί στην μέση τιμή της Y)
- Το παραπάνω μοντέλο καλείται απλό γραμμικό μοντέλο γιατί έχει μία μόνο επεξηγηματική μεταβλητή Χ.
Απλή Γραμμική Παλινδρόμηση με την R
- Για τυχαίο δείγμα \( (Y_1,X_1 ),...,(Y_n, X_n ) \) έχουμε: \[Y_i = a + bX_i + ε_i , ε_i \sim Ν(0, σ^2) \]
- Τα a, b και \(σ^2\) είναι οι άγνωστες παράμετροι του μοντέλου μας (συντελεστές μοντέλου), τις οποίες θα εκτιμήσουμε με την βοήθεια των παρατηρήσεων που διαθέτουμε που είναι οι τιμές ενός τυχαίου δείγματος.
- Η σταθερά a εκφράζει την μέση τιμή της Υ όταν το Χ=0.
- H σταθερά b εκφράζει το πόσο αναμένεται να μεταβληθεί η αναμενόμενη τιμή της Υ, αν η Χ αυξηθεί κατά μία μονάδα.
- Η ποσότητα \(σ^2\) εκφράζει την διασπορά των σφαλμάτων, την οποία θεωρούμε σταθερή ανεξάρτητα της τιμής της τ.μ. Χ (υπόθεση ομοσκεδαστικότητας) αλλά και της κατανομής της Υ δεδομένης μιας τιμής της Χ.
Απλή Γραμμική Παλινδρόμηση με την R
- Tα a και b υπολογίζονται ώστε το άθροισμα των τετραγώνων των σφαλμάτων \(\displaystyle\sum_{i=1}^{n} ε_i^2 \) να είναι ελάχιστο (μέθοδος ελαχίστων τετραγώνων).
- Εκτιμώντας λοιπόν τα a και b από τα αντίστοιχα \( \hat{a} \), \( \hat{b} \) καταλήγουμε στο \[ \hat{Y} = \hat{a} + \hat{b}X \]
- Το \( \hat{Y} \) καλείται προβλεπόμενη τιμή και είναι η αναμενόμενη τιμή που θα πάρει η Υ όταν Χ=x, όπως αυτήν την εκτιμήσαμε με βάση το μοντέλο παλινδρόμησης. Η προβλεπόμενη τιμή είναι τ.μ., δηλαδή για διαφορετικό δείγμα ενδέχεται να πάρει άλλη τιμή όταν X=x.
Απλή Γραμμική Παλινδρόμηση με την R
- Για κάθε παρατήρηση \(x_i\) μπορούμε υπολογίσουμε τις προβλεπόμενες τιμές \[ \hat{y}_i = \hat{a} + \hat{b}x_i \]
- Είναι φανερό ότι θα υπάρχει διαφορά μεταξύ της παρατηρούμενης τιμής \( y_i \) (observed) για δοσμένο \( x_i \) από την προβλεπόμενη, θεωρητική (που προκύπτει από το μοντέλο) (predicted) \( \hat{y}_i = \hat{a} + \hat{b}x_i (predicted)\).
- Η διαφορά αυτή είναι τα \( ε_i \) δηλ. \[ ε_i= y_i-\hat{y}_i \] που λέγονται υπόλοιπα (residuals).
Απλή Γραμμική Παλινδρόμηση με την R
- Tα \( ε_i \) είναι η διαφορά της παρατηρούμενης τιμής \( y_i \) (observed) για δοσμένο \( x_i \) από την προβλεπόμενη, θεωρητική (που προκύπτει από το μοντέλο) (predicted) τιμή \( \hat{y}_i = \hat{a} + \hat{b}x_i (predicted)\) δηλ. \[ ε_i= y_i-\hat{y}_i \] και λέγονται υπόλοιπα (residuals).
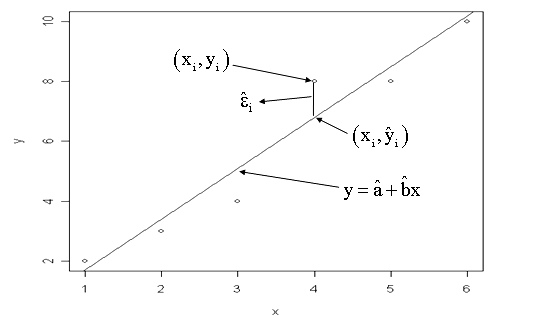
Απλή Γραμμική Παλινδρόμηση με την R
- Το \(σ^2\) εκτιμάται από το \[s^2=\frac{1}{n-2}\displaystyle\sum_{i=1}^{n} (y_i-\hat{y}_i)^2 \] και καλείται μέσο τετραγωνικό σφάλμα (MSE)
- Η θετική τετραγωνική ρίζα του \(s^2\) είναι το τυπικό σφάλμα της παλινδρόμησης. Είναι ουσιαστικά η μέση απόκλιση μεταξύ της πραγματικής και της εκτιμούμενης τιμής της y.
- Όσο πιο μικρό τυπικό σφάλμα ---> καλύτερο μοντέλο
Απλή Γραμμική Παλινδρόμηση με την R
- Μέτρο που δείγχει πόσο καλό είναι το μοντέλο είναι ο συντελεστής προσδιορισμού \(R^2\) (R-squared). \[ R^2=1-\frac{\displaystyle\sum_{i=1}^{n} (y_i-\hat{y}_i)^2}{\displaystyle\sum_{i=1}^{n} (y_i-\overline{y})^2}, 0 ≤ R^2 ≤ 1 \]
- Εκφράζει το ποσοστό της διαποράς του Y που εξηγείται από το μοντέλο παλινδρόμησης
- \(0 ≤ R^2 ≤ 1\).
Απλή Γραμμική Παλινδρόμηση με την R
- Όσο πιο μεγάλο το \(R^2\) ----> τόσο ισχυρότερη η γραμμική συσχέτιση.
- Εμπειρικά, τιμές του \(R^2\) μεγαλύτερες του 70% υποδεικνύουν ικανοποιητικά μοντέλα και τιμές πάνω από 90% υποδεικνύουν μοντέλα με πολύ καλύ προσαρμοστικότητα.
- Στην απλή γραμμική παλινδρόμηση το \(R^2\) ισούται με το τετράγωνο του δειγματικού συντελεστή συσχέτισης r.
- Το \(R^2\) μας δείχνει την καλή προσαρμογή του μοντέλου και όχι πόσο καλή πρόβλεψη κάνει το μοντέλο.
Απλή Γραμμική Παλινδρόμηση με την R
- Επειδή οι εκτιμήσεις των a και b του μοντέλου γίνονται με βάση το δείγμα που έχουμε μας ενδιαφέρει να ελέγξουμε τις υποθέσεις:
- \( Η_0 \): b=0 έναντι της εναλλακτικής \(Η_1\) : b ≠ 0
- \( Η_0 \) : a=0 έναντι της εναλλακτικής \(Η_1\) : a ≠ 0.
- Μας ενδιαφέρει πρωτίστως να ελέγξουμε την υπόθεση \( Η_0 \): b=0 γιατί αν ισχύει αυτή η υπόθεση τότε το μοντέλο γίνεται Y=a που σημαίνει ότι η τιμή της μεταβλητής Y είναι ανεξάρτητη από την τιμή της μεταβλητής Χ.
- Οι ελεγχοσυναρτήσεις και των δύο παρπάνω ελέγχων ακολουθούν St(n-2) κατανομή.
Απλή Γραμμική Παλινδρόμηση με την R
- Ένας άλλος έλεγχος που συνήθως εξετάζουμε στο μοντέλο παλινδρόμησης είναι γνωστός με την ονομασία F-test (ακολουθεί την F(1,n-2) κατανομή), ο οποίος ελέγχει κατά πόσο το προτεινόμενο μοντέλο y=a+bx διαφέρει από το σταθερό y=a. Στη απλή γραμμική παλινδρόμηση ο έλεγχος αυτός είναι ισοδύναμος με τον έλεγχο για το b που είδαμε πριν. Δηλ. \( Η_0 \): b=0 έναντι της εναλλακτικής \(Η_1\) : b ≠ 0
Απλή Γραμμική Παλινδρόμηση με την R
- Από το απλό γραμμικό μοντέλο μπορούμε να εκτιμήσουμε τη μέση τιμή του y, για δοσμένη τιμή του x. To \(100(1-a)\%\) δ.ε για την μέση τιμή του y ονομάζεται διάστημα εμπιστοσύνης (confidence interval)
- Αν όμως θέλουμε να προβλέψουμε την τιμή του y, για δοσμένη τιμή του x τότε χρησιμοποιούμε το \(100(1-a)\%\) δ.ε για την πρόβλεψη του y που είναι διαφορετικό και ονομάζεται διάστημα πρόβλεψης (prediction interval)
- To διάστημα πρόβλεψης (prediction interval) περιέχει το αντίστοιχο διάστημα εμπιστοσύνης (confidence interval) γιατί η πραγματική τιμή του y, έχει μεγαλύτερη διασπορά από τη μέση τιμή.
Απλή Γραμμική Παλινδρόμηση με την R
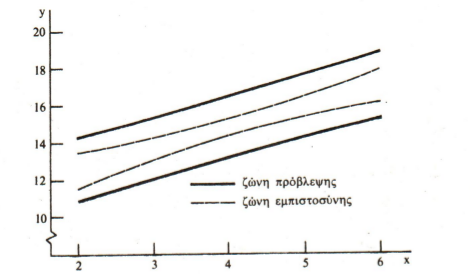
- Για κάθε τιμή του x βρίσκουμε ένα διάστημα εμπιστοσύνης. Αν κάνουμε την γραφική παράσταση των ορίων των διαστημάτων εμπιστοσύνης και ενώσουμε όλα τα κατώτερα όρια και όλα τα ανώτερα όρια, παίρνουμε μια \(100(1-a)\%\) ζώνη εμπιστοσύνης. Ομοίως μπορεί να κατασκευαστεί και μια ζώνη πρόβλεψης.Οι ζώνες φαίνονται παρακάτω:
Προϋποθεσεις απλού γραμμικού μοντέλου
- Γραμμικότητα
- Κανονικότητα Σφαλμάτων
- Ομοσκεδαστικότητα : Γραφική παράσταση των υπολοίπων συναρτήσει των προβλεπόμενων τιμών ή συναρτήσει των τιμών της Χ. Τα ζεύγη αυτών των τιμών δεν πρέπει να εμφανίζουν κάποιο συστηματικό τρόπο συμπεριφοράς.
- Ανεξαρτησία Σφαλμάτων: Κατασκευάζουμε ένα διάγραμμα υπολοίπων σε σχέση με την σειρά των δεδομένων, στο οποίο δεν πρέπει να παρουσιάζεται κάποια σχέση και τα υπόλοιπα να συμπεριφέρονται τυχαία.
Παράδειγμα απλού γραμ. μοντέλου στην R
- Θα προσπαθήσουμε να βρούμε ένα μοντέλο που να μπορεί να μας δώσει την τιμή της απόστασης που ακινητοποιείται το αυτοκίνητο δεδομένου ότι ξέρουμε την ταχύτητα του.
- Το απλό γραμμικό μοντέλο \[Y = a + bX + ε , \] με \( ε \sim Ν(0, σ^2) , \) στην περίπτωση μας γίνεται: \[car$dist=a + b * car$speed + ε ,\]
- Το μοντέλο υπολογίζεται στην R από την συνάρτηση lm().
Παράδειγμα απλού γραμ. μοντέλου στην R
- Η συνάρτηση lm() μας δίνει το αντικείμενο του γραμμικού μοντέλου όπου μεταξύ άλλων περιέχει τους συντελεστές (coefficients) a και b της ευθείας
> lm_car<-lm(cars$dist~cars$speed) # ή
> lm_car<-lm(dist~speed, data=cars) # πιο σωστό
> lm_car
Call:
lm(formula = dist ~ speed, data = cars)
Coefficients:
(Intercept) speed
-17.579 3.932Παράδειγμα απλού γραμ. μοντέλου στην R
- Αποθηκεύοντας το αποτελέσμα της συνάρτηση lm() σε ένα το αντικείμενο (lm_car) έχω διαθέσιμα τα αποτελέσματα.
> attributes(lm_car)
$names
[1] "coefficients" "residuals" "effects" "rank" "fitted.values" "assign"
[7] "qr" "df.residual" "xlevels" "call" "terms" "model"
$class
[1] "lm"Παράδειγμα απλού γραμ. μοντέλου στην R
- Μπορούμε να πάρουμε τους συντελεστές a και b και τα υπόλοιπα με δύο τρόπους:
> lm_car$coefficients
(Intercept) speed
-17.579095 3.932409
> coefficients(lm_car)
(Intercept) speed
-17.579095 3.932409
> lm_car$residuals[1:5]
1 2 3 4 5
3.849460 11.849460 -5.947766 12.052234 2.119825
> residuals(lm_car)[1:5]
1 2 3 4 5
3.849460 11.849460 -5.947766 12.052234 2.119825 Παράδειγμα απλού γραμ. μοντέλου στην R
- Μπορούμε να πάρουμε τις τιμές των αποστάσεων που υπολογίζονται με βάση το μοντέλο:
> lm_car$fitted.values[1:5]
1 2 3 4 5
-1.849460 -1.849460 9.947766 9.947766 13.880175
> fitted.values(lm_car)[1:5]
1 2 3 4 5
-1.849460 -1.849460 9.947766 9.947766 13.880175
> predict(lm_car)[1:5]
1 2 3 4 5
-1.849460 -1.849460 9.947766 9.947766 13.880175 Παράδειγμα απλού γραμ. μοντέλου στην R
- Μπορούμε να πάρουμε τα διαστήματα εμπιστοσύνης για την αναμενόμενη τιμή του dist και τα διαστήματα πρόβλεψης για το dist όταν speed=27 και speed=30:
> predict(lm_car, interval = "confidence")
fit lwr upr
1 -1.849460 -12.329543 8.630624
2 -1.849460 -12.329543 8.630624
3 9.947766 1.678977 18.216556
4 9.947766 1.678977 18.216556
5 13.880175 6.307527 21.452823
.......................................
48 76.798715 68.387653 85.209778
49 76.798715 68.387653 85.209778
50 80.731124 71.596083 89.866166
> predict(lm_car, list(speed=c(27,30)), interval="predict")
fit lwr upr
1 88.59594 55.89643 121.2955
2 100.39317 66.86529 133.9210Παράδειγμα απλού γραμ. μοντέλου στην R
- Προσθέτουμε στο γράφημα την ευθεία που υπολογίστηκε από το μοντέλο lm_car
> plot(cars$speed, cars$dist, main="Speed versus Stopping distance", pch=16, col=2, xlab="Speed", ylab="Stopping Distance")
> abline(lm_car, lwd=2)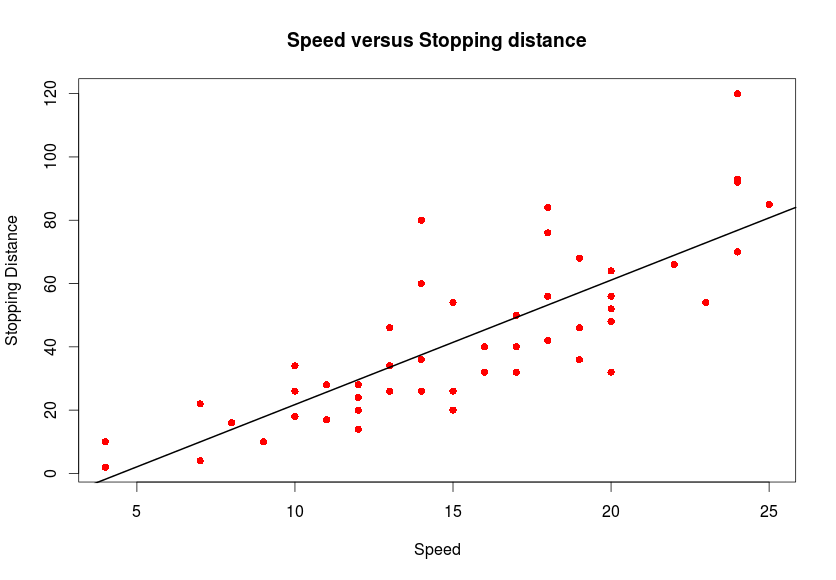
Aπό το όρισμα lm_car παίρνει τους συνετελεστές της ευθείας lm_car. Με το lwd δίνουμε το πάχος της ευθείας.
Παράδειγμα απλού γραμ. μοντέλου στην R
- Στο προηγούμενο γράφημα μπορούμε να προσθέσουμε τα σημεία που υπολογίζονται από το μοντέλο
> points(cars$speed,predict(lm_car), col="green")
Τα σημεία που υπολογίζονται από το μοντέλο τα χρωματίσαμε πράσινα.
Παράδειγμα απλού γραμ. μοντέλου στην R
- Αναλυτικά τα αποτελέσματα του γραμμικού μοντέλου τα παίρνουμε δίνοντας:
> summary(lm_car)
Call:
lm(formula = dist ~ speed, data = cars)
Residuals:
Min 1Q Median 3Q Max
-29.069 -9.525 -2.272 9.215 43.201
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -17.5791 6.7584 -2.601 0.0123 *
speed 3.9324 0.4155 9.464 1.49e-12 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 15.38 on 48 degrees of freedom
Multiple R-squared: 0.6511, Adjusted R-squared: 0.6438
F-statistic: 89.57 on 1 and 48 DF, p-value: 1.49e-12Παράδειγμα απλού γραμ. μοντέλου στην R
- Παρατηρούμε ότι για το μοντέλο μας \[dist=-17.579 + 3.932speed + ε_i \] έχουμε:
- Ο συντελεστής προσδιορισμού \(R^2=0.6511\) όχι πολύ καλός αλλά ούτε και απαγορευτικός.
- Ο διορθωμένος συντελεστής προσδιορισμού Adjusted R-squared μας ενδιαφέρει όταν έχουμε παραπάνω από μία επεξηγηματικές μεταβλητές.
- Το τυπικό σφάλμα s=15.38 για 48 βαθμούς ελευθερίας δεν είναι μικρό.
Παράδειγμα απλού γραμ. μοντέλου στην R
- Ωστόσο, ο συντελεστής b της speed είναι στατιστικά σημαντικός για όλα τα a (η p-value είναι πολύ μικρή) δηλαδή, απορρίπτεται η μηδενική υπόθεση που ισχυρίζεται ότι b=0 και επομένως η ταχύτητα σχετίζεται γραμματικά με την απόσταση ακινητοποίησης του αυτοκινήτου. Ακριβώς τα ίδια προκύπτουν και από το F στατιστικό.
- Ο σταθερός όρος του μοντέλου (Intercept) είναι στατιστικά σημαντικός όχι όμως για όλα τα a (p-value=0.0123) άρα ίσως και να μπορεί να παραληφθεί.
Παράδειγμα απλού γραμ. μοντέλου στην R
-
Προϋποθέσεις του μοντέλου:
- Γραμμικότητα: Ελέγχθηκε με το διάγραμμα της διασποράς
- Κανονικότητα Σφαλμάτων:
> par(mfrow=c(2,2))
> hist(lm_car$residuals)
> par(mfrow=c(1,2))
> hist(lm_car$residuals)
> qqnorm(lm_car$residuals)
> qqline(lm_car$residuals)
> par(mfrow=c(1,1))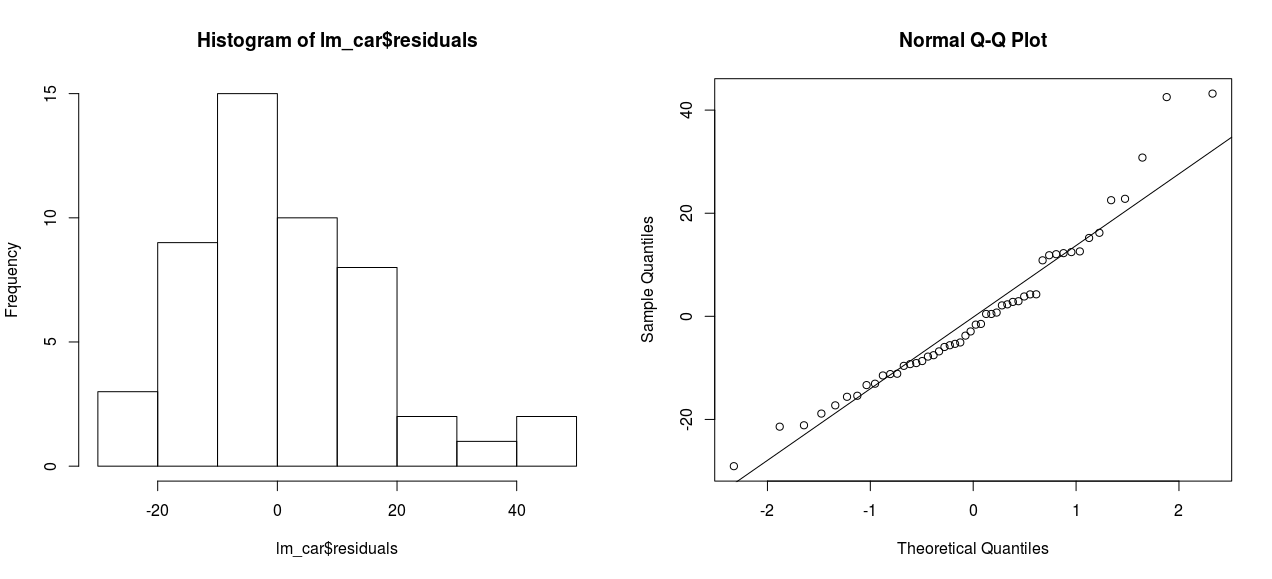
Παράδειγμα απλού γραμ. μοντέλου στην R
-
Προϋποθέσεις του μοντέλου:
- Κανονικότητα Σφαλμάτων (συνέχεια):
> library("nortest")
> lillie.test(lm_car$residuals)
Lilliefors (Kolmogorov-Smirnov) normality test
data: lm_car$residuals
D = 0.12957, p-value = 0.03529Παράδειγμα απλού γραμ. μοντέλου στην R
-
Προϋποθέσεις του μοντέλου:
- Ομοσκεδαστικότητα : Γραφική παράσταση των υπολοίπων συναρτήσει των προβλεπόμενων τιμών ή συναρτήσει των τιμών της Χ. Τα ζεύγη αυτών των τιμών δεν πρέπει να εμφανίζουν κάποιο συστηματικό τρόπο συμπεριφοράς.
> par(mfrow=c(1,2))
> plot(lm_car$residuals, lm_car$fitted.values)
> plot(lm_car$residuals,cars$speed)
> par(mfrow=c(1,1))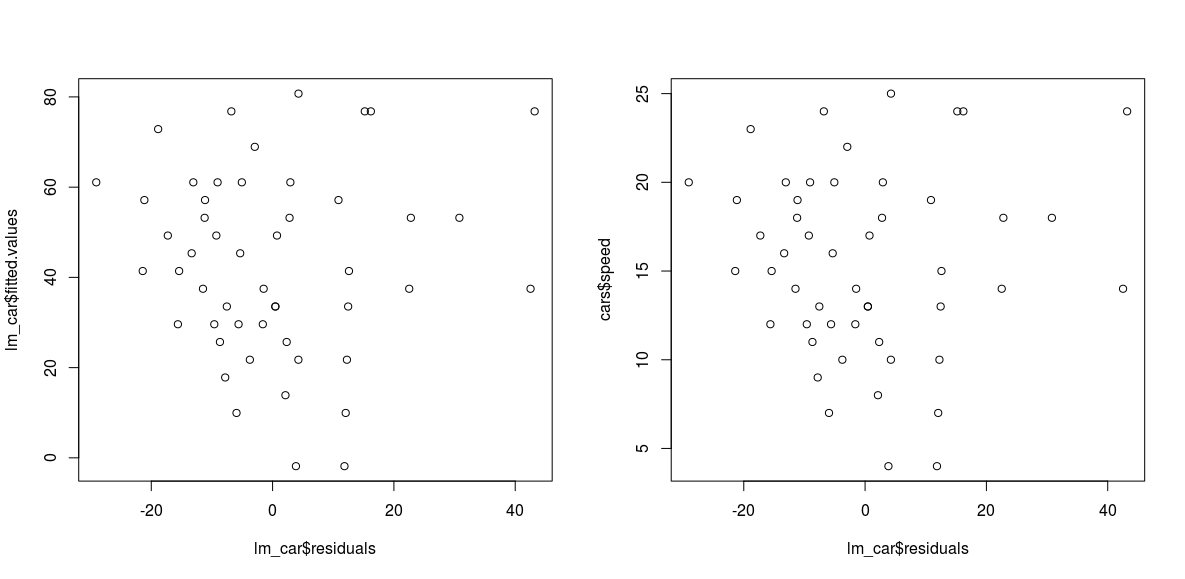
Παράδειγμα απλού γραμ. μοντέλου στην R
-
Προϋποθέσεις του μοντέλου:
- Ανεξαρτησία Σφαλμάτων: Κατασκευάζουμε ένα διάγραμμα υπολοίπων σε σχέση με την σειρά των δεδομένων, στο οποίο δεν πρέπει να παρουσιάζεται κάποια σχέση και τα υπόλοιπα να συμπεριφέρονται τυχαία.
> plot(1:50,lm_car$residuals)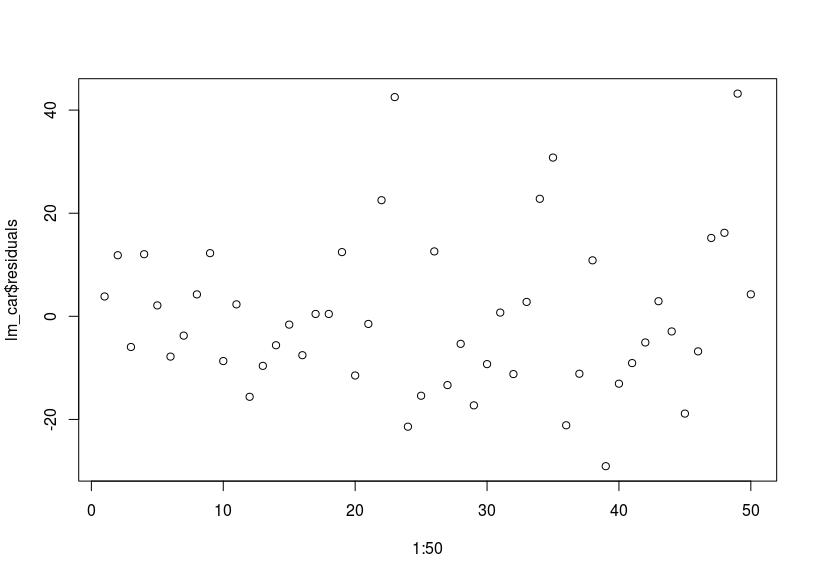
Παράδειγμα απλού γραμ. μοντέλου στην R
- Ενδεικτικά αναφέρουμε ότι ένας λογαριθμικός μετασχηματισμός και για τις δύο μεταβλητές θα βελτίωνε πολύ τα αποτελέσματα του μοντέλου αλλά και τις προϋποθέσεις του.
> lm_logcars<-lm(log(dist)~log(speed), data=cars)
> lm_logcars
Call:
lm(formula = log(dist) ~ log(speed), data = cars)
Coefficients:
(Intercept) log(speed)
-0.7297 1.6024
> summary(lm_logcars)
Call:
lm(formula = log(dist) ~ log(speed), data = cars)
Residuals:
Min 1Q Median 3Q Max
-1.00215 -0.24578 -0.02898 0.20717 0.88289
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.7297 0.3758 -1.941 0.0581 .
log(speed) 1.6024 0.1395 11.484 2.26e-15 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.4053 on 48 degrees of freedom
Multiple R-squared: 0.7331, Adjusted R-squared: 0.7276
F-statistic: 131.9 on 1 and 48 DF, p-value: 2.259e-15